音频信号是一种可压缩信号,借助压缩感知理论可以进行数据压缩并高度准确地重建。存在的问题是音频信号在典型正交基上不稀疏,给重建带来挑战。音频信号的语谱图的能量呈现块状分布,这种分布适合用马尔可夫随机场来建模。借助这种模型,我们获得了较高的重建精度。整个算法的框架如图1所示。
图1音频信号压缩采样和重建框图
首先,对音频的MDCT系数的先验分布进行建模。
选取一段音频信号做加窗MDCT变换,得到系数矩阵,其维度为N×T。
音频信号MDCT系数大部分接近于零,仅有少量系数较大而且在时频图上连续分布为块状。基于这种事实,每个系数的先验分布用伯努利-高斯模型表示:
(1)
为稀疏率。
进一步用隐变量表示为
(2)
为支撑(support),它的状态可取值,为幅度。
其次,对音频MDCT系数之间的关系进行建模。
音频信号是时变信号,但是在相邻两帧处频率成分变化不大;同时在单帧内相邻频率成分能量接近。音频MDCT系数这种分布特性可以用其支撑变量构成的马尔可夫随机场来表示。其中支撑与,沿时间轴相连,与,沿频率轴相连。这四个变量构成的邻域,记为。维的支撑集记为,它的概率分布可以表示为:
(3)
即伊辛模型(Ising model)。表示交互作用参数,任意相邻支撑变量的交互参数相同;表示稀疏度,不同支撑变量稀疏度不同。
支撑变量构成的马尔可夫随机场部分区域如图2所示。
图2 马尔可夫随机场的部分图
在随机场沿时间轴和频率轴执行消息传递,这样可以利用相邻MDCT系数的连续性对各支撑变量进行状态更新,这是提高重建精度的关键。考虑到算法复杂度,本发明假设相邻系数的幅度不相关。
再次,对系数矩阵进行压缩采样,并对采样过程用因子图表示。
压缩采样通过对系数矩阵左乘一个欠定线性方程来实现,这样做相当于将每帧MDCT系数投影到较低维度的向量上,在保存原始信号信息的同时进行了数据压缩。用方程表示如下:
(4)
其中为欠定测量矩阵,维度为M×N(M<N);为测量噪声;(M×T)为压缩采样值,通常称为测量值。
压缩采样的过程可以用图3的因子图表示。其中圆圈表示变量节点,方框表示函数节点。观测变量已知,其包含于相应的函数节点中。为的一个元素。由于可以由其隐变量和表示,这三个变量通过函数节点相连。表示的分布。各变量和函数的下标的第一个数字表示系数对应的频率成分,第二个数字表示系数所在的帧。每一帧系数的压缩采样示于图3 的各矩形框内。每一帧系数的维度为N×1,通过左乘测量矩阵得到M×1维的测量值,这种非自适应线性采样过程如图3中各方框内的连接线所示。其中系数位于右侧,测量值位于左侧。另外可以看到函数节点的变量之一的支撑变量在右边伸出,所有时频点的支撑变量在阴影部分形成马尔可夫随机场,其详细结构示于图2。基于以上的因子图,恢复系数矩阵的工作可以通过消息传递的方式来实现。
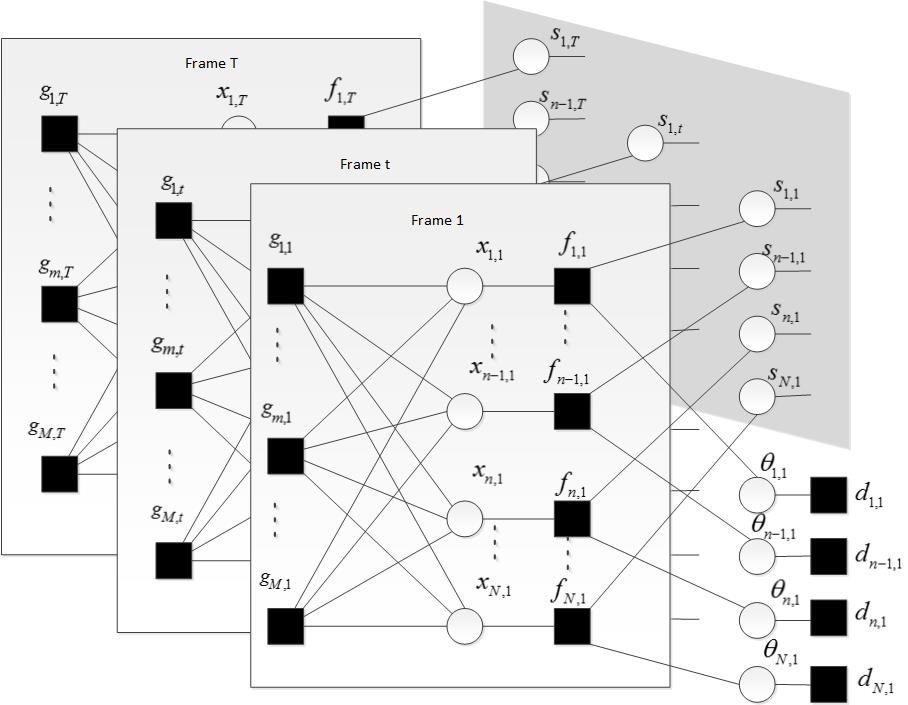
图3 音频信号压缩采样图
最后,从测量值中重建原始音频MDCT系数。
信号的重建采用一种类似Turbo均衡的迭代方式,它用到了近年提出的近似消息传递(Approximate Message Passing, AMP)算法。在信号(向量形式)稀疏的情况下,AMP算法从压缩采样(设测量矩阵维度为M×N,其中M<N)后的测量值中以O(MN)的计算复杂度精确地恢复原始信号,是目前最为高效的压缩感知重建算法之一。尽管如此,对于音频信号效果仍然不好,原因是音频信号的变换域系数不够稀疏。所以还需要利用随机场结构提高重建精度。
Turbo重建首先对系数的分布进行初始化,在各帧内执行AMP算法,它从测量值中得到原始信号的系数的后验分布。各时频点将其后验分布作为消息传递给对应的支撑和幅度,并更新后两者的信息。得到后验信息的后,分别在马尔可夫随机场上沿时间轴从左到右、从右到左执行消息传递,同样地在频率轴做消息传递。消息传递完成后的状态再次得到了更新。接着将更新后的状态信息代入易辛模型,求解使得方程(3)值最小的参数,的值。消息传递执行完成后各支撑对应的幅度和系数的分布跟着更新。随着系数分布完成更新,一轮Turbo消息传递完成。可以看出,在这一过程中AMP和马尔可夫随机场内的置信传播交替执行。如此迭代执行Turbo消息传递,当相邻两次迭代的信号估值的差小于规定的阈值或者达到一定的迭代次数后停止算法,返回信号估值。
实验结果:
表1 语音信号的压缩感知重建
| Fista | AMP | MRF | |
| SNR(dB) | 19.6017 | 21.1738 | 22.4103 |
| Runtime | 1257.18966 | 63.465364 | 160.259364 |
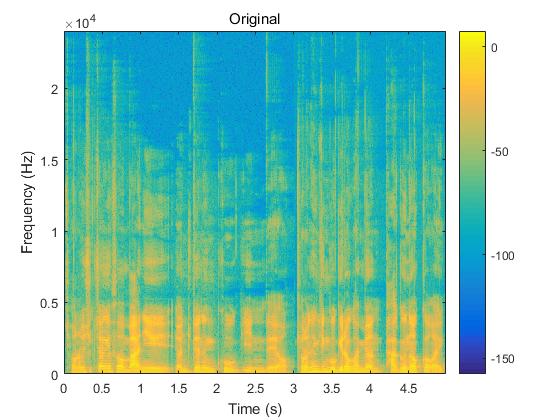
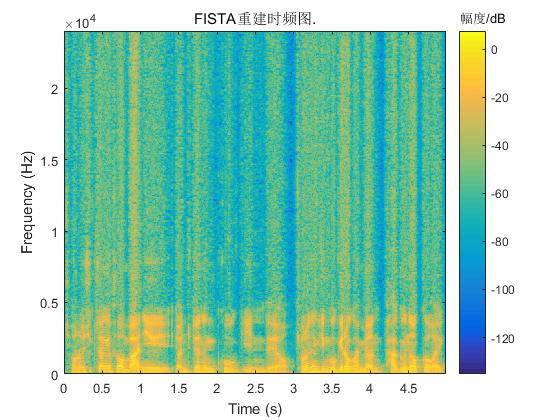
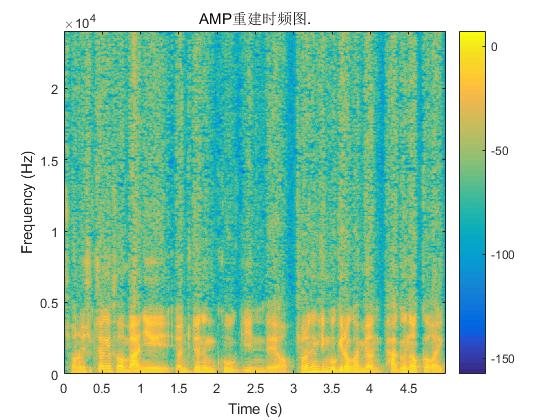
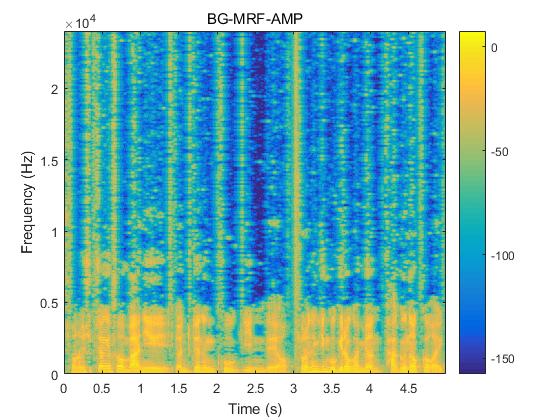
图4 语音信号原始语谱图和三种算法重建信号的语谱图
表2 乐音信号的压缩感知重建
| Fista | AMP | MRF | |
| SNR(dB) | 15.9091 | 38.4828 | 39.5917 |
| Runtime | 896.02178 | 80.726735 | 133.885270 |
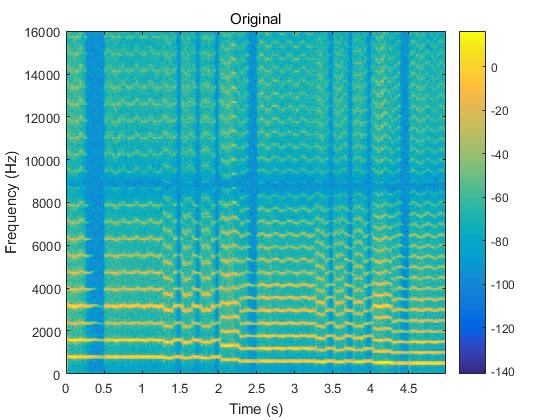
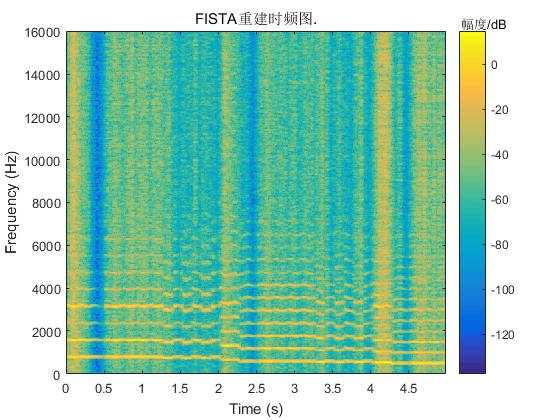
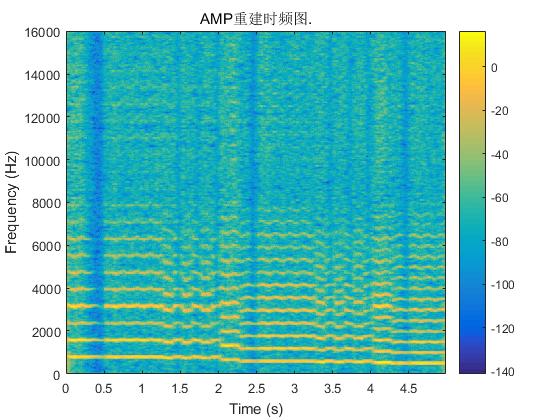
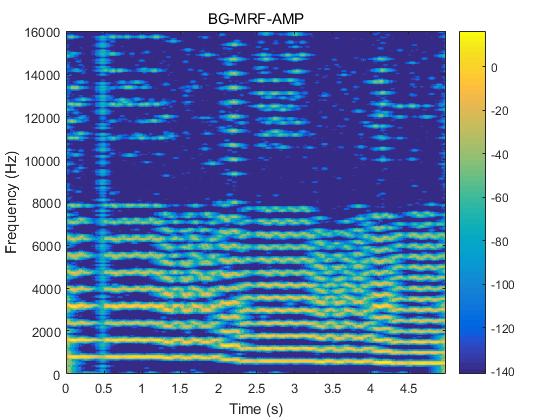
图5 乐音信号原始语谱图和三种算法重建信号的语谱图