研究背景

在高精度的定位中载波相位由于其极低的噪声以及不受多径效应影响等特点，其观测量精度能够达到厘米级，进而能够获取高精度定位结果。但载波相位由于其整周数的不确定性，即整周模糊度的存在，加大了定位算法的复杂度以及定位实时性的难度。因此本文针对载波相位的高精度定位做出研究，分析总结了载波相位的模糊度解算算法，并且对于当今的PPP-RTK定位技术的性能指标进行调研分析。结果表明，PPP-RTK技术中，宽巷以及窄巷模糊度的解算各需要10分钟，才能达到整周数固定的定位结果。其定位精度相比整周数未固定的解有了显著提升，但在实时性方面远未达到实时定位的需求，只能应用在近实时定位的应用之中。

载波相位模糊度解算策略LAMBDA算法

对于载波相位观测量可以构建双差方程即

（1）

其中为双差因子，为载波相位观测量，是未知的接收机天线坐标，是给定的卫星坐标，为信号波长，为整周模糊度，表征相位观测量的噪声以及偏差，比如电离层延时、多径等。

对于多个观测双差方程，可以构成方程组，从而可以解算其中的模糊度，将这些方程线性化并以矩阵形式表示得到

（2）

其中、、、各方程中对应观测量、整周数、基线未知量、噪声及偏差量所组成的向量。从而求解整周模糊度问题转化为一种特殊的最小二乘问题，在这一问题下，要满足待求的最小二乘解保持整数特性。

对于一般的最小二乘问题不多做赘述，而此处要满足求解的整数特性，需要使用搜索的策略，主要是在最小二乘解周围的椭圆范围内的整数格点处搜索，寻找偏差最小的整数格点。但在实际求解过程中，会发现上述策略会存在缺陷，导致算法开销极大。最为重要的一点就是由于各个方程之间的相关性极大，导致搜索的椭圆区域极为扁平，寻找整数格点的效率较低。解决这一问题的方法是对方程所对应的矩阵进行保体积、保整数特性的去相关处理，从而在不改变变换前后整数解空间的一一对应性的条件下将原来的椭圆搜索区域变为接近圆形的搜索区域，进而提高搜索效率。

PPP-RTK定位性能调研分析

普通的RTK技术是使用差分站的观测数据，通过差分来消去观测量中的共模误差项来提高定位精度，其辅助定位使用的观测站数据属于OSR(Observation Space representation)，普通的PPP技术则使用SSR(State Space representation)作为辅助定位的数据形式，可以支持更加广域的精确定位。PPP-RTK则综合了两者的特性，使用SSR的同时保持了整周模糊度的整数特性，可以进一步提升定位精度至厘米级。

PPP-RTK中的模糊度解算可以分为宽巷模糊度和窄巷模糊度两种，这里所调研的一篇文献中对此进行了详细的分析。

对于宽巷模糊度，文献中分析比较了不同仰角、不同观测时间下模糊度解算情况。在平均仰角相同情况下，观测时间越长，能够解算出的模糊度固定解个数越多；在平均仰角更高的情况下，相同观测时间下能够解算出的模糊度固定解个数更多。因此可以以平均仰角和观测时间共同作为评判解算可靠性和效率的指标。进一步的实验结果表明在以平均仰角，观测时间600秒为阈值的情况下，99.86%的模糊度都能得到固定。

对于窄巷模糊度而言，研究的指标是其小数部分收敛至波动幅值小于0.1cycle所需时间。从下图可以看出，窄巷模糊度的小数部分要收敛至波动幅值小于0.1cycle需要数十分钟的时间，随着观测时间的变长以及卫星观测仰角的提升，其波动才逐渐稳定下来。

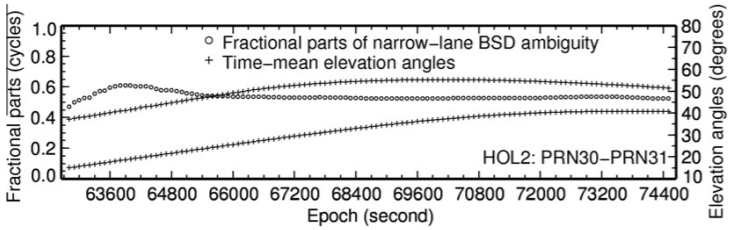
进一步分析表明观测时间10分钟的情况下，69.0%的波动幅值是大于0.1cycle的，而仅仅对于整数的解算而言，这个约束可以放宽至0.25cycle，在同样观测10分钟的条件下，87.9%的波动幅值小于0.25cycle。在这种情况下，只要宽巷模糊度已经确定，则可以由此估算出窄巷模糊度。

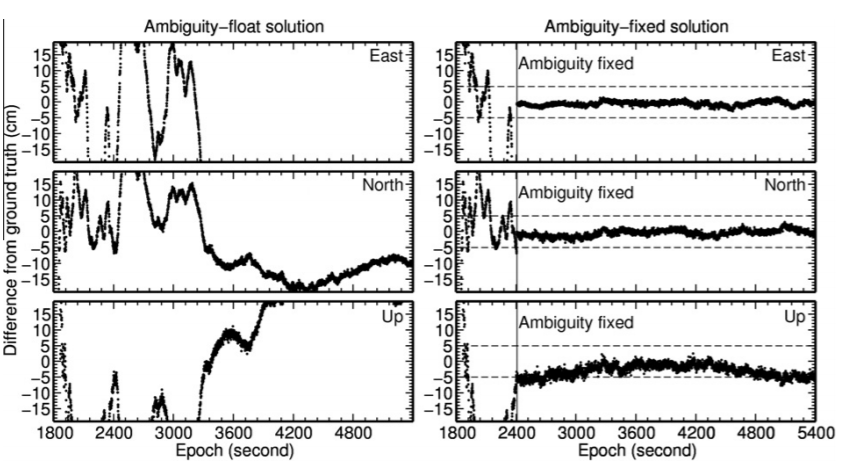
最后需要分析模糊度的固定对于最终定位结果的影响。下图展示了模糊度为浮点解以及模糊度固定的情况下，ENU方向上的定位误差。经过模糊度固定解的解算，ENU方向上的平均误差从13.1cm、7.1cm、11.4cm减小为0.8cm、0.9cm、2.5cm。另外通过下图也可以发现浮点解经过1小时也未收敛至厘米级的定位精度而固定解在600秒左右就能收敛至厘米级精度，从而可以认为模糊度的固定解的解算可以加快收敛速率。

总结

本研究主要调研了高精度载波定位中载波相位模糊度解算策略以及PPP-RTK的定位性能指标。LAMBDA载波相位解算算法主要通过去相关来提高搜索的效率以达到快速的模糊度解算，其算法在PPP-RTK中也能得到应用。在PPP-RTK的性能调研中，宽巷、窄巷的模糊度的固定解算都需要10分钟甚至更多的时间，还不能满足实时固定解解算的需求，但模糊度固定后定位精度和收敛速率都有较大提升。对于未来的研究而言，更加快速的模糊度解算策略将是达到实时PPP-RTK定位的关键技术研究点。