2016年召开的谷歌IO大会宣布开放安卓设备的原始观测量,这一消息具有重要的现实意义,由此我们可以预见在未来不久使用低成本设备就可以体验到更高精度的基于位置的服务。
现如今,智能手机中的超低成本GNSS芯片有着诸如低功耗、低性能天线和计算资源受限等特性,所以它远不能和测绘级或商业级GNSS接收机媲美。我们团队关注了低功耗GNSS芯片的间歇模式对载波观测量的影响,并系统地讨论了重建间歇载波观测量的可行性,这对于实现基于低成本移动设备的高精度定位具有重要意义。
研究方法
在我们的研究中,重点用三种方法分析了ADR的相位观测量:
- 码相位减载波相位: 码相位解算而来的伪距是一种绝对测量值并且不依赖于对信号的连续跟踪,所以间歇模式对伪距观测量几乎没有任何影响。在长时间连续观测下,伪距和ADR的趋势可以通过对二者做差进行比较。
- 周跳检测: 传统周跳问题主要是信号丢失、阻塞和接收机硬件故障导致的,所以周跳检测的原理是检测这些观测量在时间上的不连续性,并且由此估计周跳大小。间歇模式将导致不连续的载波相位跟踪,但这是否是一种传统的周跳问题仍然有待商榷。
- 短基线单差后处理: 这种方法首先建立一个单差观测模型,然后基于先验信息,比如基准站和流动站的真实位置、接收机钟偏和钟飘等,从原始观测量中分离出观测误差。最后,这种方法估计了连续时的载波相位观测量,并和原始载波相位观测量进行对比。
- 安卓设备中的GNSS芯片的间歇模式的模型如下:
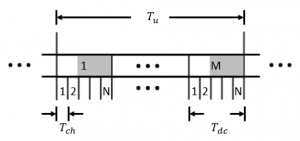
在GNSS基带信号处理中有三种不同的时间概念,分别描述如下:
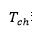 称作积分清除时间,是最基本的信号处理单元并且不能再分。
称作积分清除时间,是最基本的信号处理单元并且不能再分。
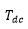 称作占空比时间。它包含N个
称作占空比时间。它包含N个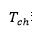 这一时间分为工作时间
这一时间分为工作时间  和睡眠时间
和睡眠时间 。
。  包含前 k 个
包含前 k 个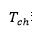 , 而
, 而 包含剩余的 N-k 个
包含剩余的 N-k 个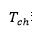 ,其中k也是整数。
,其中k也是整数。- 间歇信号处理中的间歇比定义如下:
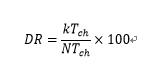
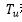 称作历元时间。它是GNSS观测量的更新间隔时间,并且它包含M个
称作历元时间。它是GNSS观测量的更新间隔时间,并且它包含M个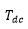 ,其中M是整数。这个时间反映了这段时间内输入信号的平均多普勒。
,其中M是整数。这个时间反映了这段时间内输入信号的平均多普勒。
如果DR等于100%,称作为连续跟踪模型,如果DR小于100%,称之为间歇跟踪模型:
对于连续跟踪模型,只有环路滤波器和NCO(数控振荡器)需要在每个积分清除时间进行更新,而其他模块无需变化。环路滤波器只更新内部积分器的结果,而滤波器参数保持不变。NCO在每个![]() 调整输出频率并且保持本地载波的相位连续。因为没有睡眠时间,PLL在每个历元时间的载波跟踪没有中断,因此本地NCO信号很好地复制了输入信号;
调整输出频率并且保持本地载波的相位连续。因为没有睡眠时间,PLL在每个历元时间的载波跟踪没有中断,因此本地NCO信号很好地复制了输入信号;
对于间歇跟踪模型,DR通常取一个小值,如10%,以此来尽量降低功耗。在![]() 时间段,此时与连续跟踪模型相同。但是,在
时间段,此时与连续跟踪模型相同。但是,在![]() 时间段,NCO会继续以上次的
时间段,NCO会继续以上次的 ![]() 产生本地复制信号,而且环路滤波器中积分器的结果也会与之前的结果保持一致。
产生本地复制信号,而且环路滤波器中积分器的结果也会与之前的结果保持一致。
在这种间歇模式下,将对ADR测量值造成很大的负面影响,主要包括一下两个方面:
间歇模式对载波跟踪造成了一些负面影响,主要包括以下两个方面:1)由于卫星和接收机之间的相对运动,载波多普勒一直在变化。 间歇模式会导致测量误差,因为它无法测量休眠时间内的多普勒变化,更糟糕的是,此误差随时间累积。 2)由于环路滤波器中的积分器在休眠时间内无法更新,因此在重新进入时会发生锁定丢失,并且环路滤波器的输出会产生过冲。 这两个原因导致ADR观测中的测量误差,随着时间的推移,这种破坏性影响变得更加严重。 这种现象称为连续失周。
针对以上问题我们团队提出了如下的载波重建的思想:基于多普勒是ADR的导数,且认为离散的多普勒样本在很短的时间内是线性变化的这一基本事实,重采样离散多普勒以获得多普勒校正,然后使用多普勒校正来重建ADR测量。 我们的方法首先获得基线矢量的准确先验值,然后使用经典的LAMBDA算法来固定浮点解。 如果未重建原始ADR测量,则双差整周模糊度会一直变化。 相反,如果重建算法有效,则固定解在一段时间内接近常数,这意味着得到方差很小的结果。
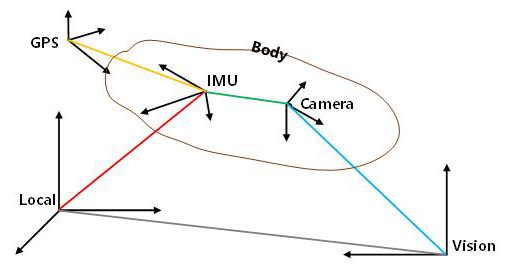
实验环境
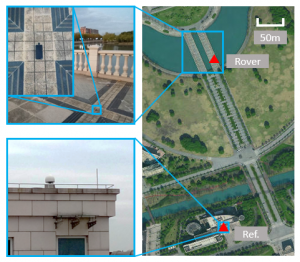
实验环境分布如上图,参考站天线的位置是先前已知的。首先,需要校准流动站的位置。 参考站是NovAtel的PP6接收机,而流动站是NovAtel的PP6D接收机,基线长度约为400米。使用Waypoint Inertial Explorer软件处理数据并获得具有厘米级精度的流动站位置。 然后,我们使用华为P10智能手机代替流动站,同时使用参考PP6接收器收集原始静态数据。
实验结果
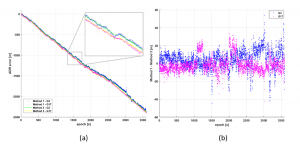
图1. 码相位减载波相位vs. 短基线单差后处理
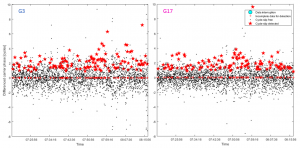
图2. 周跳检测结果
图1和图2显示了对于同一组数据从上述三种方法获得的分析结果。两颗卫星观测下的方法1和3的实验结果如图1.a所示,所有这些结果表明原始ADR与实际距离之间的偏差将随时间累积,偏差约为-0.67 m / s。 图1.b描绘了G3和G17的两种方法之间的差异,很明显,方法1比方法3更粗糙,这源于伪距的噪声。 图2显示了使用4阶差分法对G3和G17进行周跳检测的结果,它们分别在约1小时内产生122(G3)和112(G17)周跳。 周跳的次数超过了阈值(3%),这表明原始测量中存在非常不寻常的问题,但这些不规则的周跳无法帮助找出潜在问题的原因。 基于以上分析,我们认为智能手机的ADR测量问题不是传统的周跳问题。
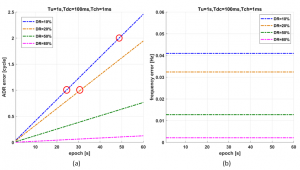
图3. 由于相对运动导致的ADR和多普勒误差
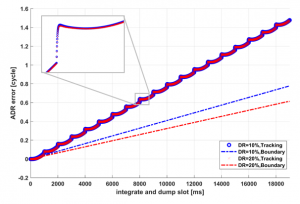
图4. 频繁失锁导致的跟踪误差
图3.a显示了不同DR的ADR误差的模拟结果,测试信号的多普勒在一分钟内从10Hz变为70Hz。 很明显,当DR相对较小时,在很短的时间内会丢失几个整数周期(参见图3.a中所示的红色圆圈)。 此外,当DR变小时,周跳的损失变大。 图3.b显示了不同DR的多普勒误差,很容易看出多普勒误差非常小并且不会累积。
我们定义进入时间为从工作时间到休眠时间的时刻,再入时间被定义为从休眠时间到工作时间的时刻。在进入时间,环路滤波器中的积分器中断积分操作。在再入时间,PLL未能锁定信号并由于不完整的积分而返回到牵入状态。在大多数情况下,![]() 比牵入时间长,即
比牵入时间长,即![]() 期间,PLL将从牵入状态重新进入锁定状态。因此,在间歇跟踪模型中,PLL将在三种状态中循环:牵入,锁定和休眠。这种频繁的状态切换也会导致周期丢失,因为当PLL处于牵入状态时,环路滤波器的输出频率差异不准确。图4显示了两种不同DR(10%和20%)下的模拟结果。与误差下边界相比,跟踪误差有两个不同,一个是明显的过冲,另一个是较大的斜率。如上所述,这些是PLL中频繁失锁的结果。
期间,PLL将从牵入状态重新进入锁定状态。因此,在间歇跟踪模型中,PLL将在三种状态中循环:牵入,锁定和休眠。这种频繁的状态切换也会导致周期丢失,因为当PLL处于牵入状态时,环路滤波器的输出频率差异不准确。图4显示了两种不同DR(10%和20%)下的模拟结果。与误差下边界相比,跟踪误差有两个不同,一个是明显的过冲,另一个是较大的斜率。如上所述,这些是PLL中频繁失锁的结果。
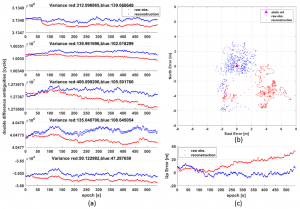
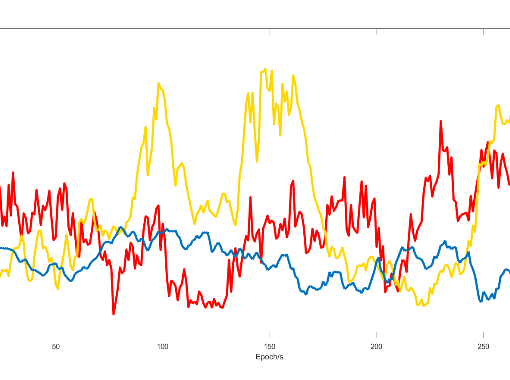
图5. 由重建ADR观测量计算得到的双差模糊度和基线矢量
图5.a显示了实验中五组双差整周模糊度的固定解,其中红色代表重建前的结果,蓝色代表重建后的结果。几组红色结果表现了时间漂移的特征,但其他组不明显,主要是因为原始ADR测量也如多径效应等受其他因素影响。与红色结果相比,时间漂移蓝色结果的特征非常小,基本上保持在一个恒定的范围内,从它们的方差可以看出。在这个静态测试中,通过使用后处理可以获得双差整周模糊度的准确估计,因此我们可以计算重建前后的基线矢量,如图5.b和图5.c所示。红色结果显示基线解与静态参考之间存在偏差,而蓝色结果主要位于半径约3m的静态参考圆中。
经过实验结果表明,原始ADR测量不仅受到间歇跟踪的影响,还受到噪声,多路径等其他严重问题的影响,因此仍需要做很多工作才能将精度提高到厘米级,实现厘米级的高精度定位,我们实验室团队接下来也将进一步研究实现高精度定位的更多有效方法。