神经形态硬件的一个重要目标是支持用户手中的快速片上学习。它需要解决两个问题:
- 一个能够在片上运行的足够强大的学习方法。
- 理想情况下只需要少量样本就能够在片上学习上快速收敛（少样本学习)。
从生物学的角度出发，人类通过不断地进化，大脑能够从一个或很少的例子中学习一个新的类。例如，我们只要看一次，或者至少看几次，就可以在许多方向、尺度和光照条件下识别一张新面孔。但是大脑能够实现快速学习是因为大脑中的神经网络在进化、发育过程中被不断优化过。并且，我们大脑的学习和泛化能力是由先天知识支持的，例如我们具备关于物体的基本属性、三维空间的知识。因此，与之前大多数神经形态芯片的学习实验不同，大脑中的神经网络在学习新事物时不会从白板状态开始[1]。
大多数类脑芯片都采用递归形式的SNN (RSNN)，我们也通常认为大脑使用递归这种结构，它的优势在于，首先递归网络在具有强时间关联性的任务表现很好，例如我们对环境做出更加精确的描述或反应，其实是接收来自许多感官信息，随着时间推移，我们拼凑这些不同类型的信息。此外，神经活动从一个神经元传播到另一个神经元需要10毫秒的时间，对于生物神经网络，由于神经信号传递的速度的限制，想要实现快速识别只能传递更少的层[2]。像我们视觉皮层虽然只有6个层，但它们具有横向、反馈连接的不同连接，从时间上展开后等价于一个超深的前向网络。因此，递归神经网络通过考虑每个计算时间步长，可以用相对小的模型实现超深度网络的精度。在机器学习领域， RNN 的学习采用随时间反向传播 (BPTT)进行训练。对于不连续（不可导）的 SNN，使用适当的代理梯度（伪梯度），BPTT 也可用于 RSNN 的训练，并在多种任务上达到了理想效果。
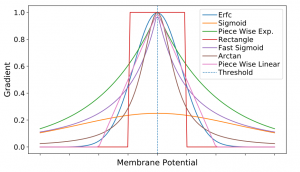图1. 不同的代理梯度函数
图2. BPTT在网络的展开版本中计算梯度
反向传播可用于通过梯度下降最小化神经网络的损失函数，随时间反向传播只是对BP的扩展，我们把循环神经网络沿时间方向虚拟展开，如图2所示，每个时间步都由这个循环网络的拷贝副本表示，并且这个网络在一个时间步产生的输出，将被发送到下一个时间步的副本，所以需要经过一段时间的计算。然后，我们实际上想最小化损失函数E，只要将BP应用于这个展开的神经网络，这就带来了一个问题，它要求必须存储与计算不同时间步对应的所有中间状态，因为当计算损失函数时，需要传播从最后一个计算时间开始的梯度，它随着时间的推移而倒退，这使得大脑实际上不可能实现这样的学习算法。
因此，面对流式数据的在线学习任务时，BPTT 存在以下显著的局限性：(1) BPTT 要求存储所有神经元的中间状态，并基于所有这些中间状态对时间上展开的网络进行反向梯度计算。随着输入序列长度的增加，在时间上展开的网络深度也线性增加。这使得 BPTT 难以在片上实现。(2)当反向传播应用于连续的数据流时，因为反向传播方法在每次更新时都会修改每个突触的权重，导致先前学习信息的遗忘，因此出现了记忆稳定性问题。反向传播覆盖先前学习任务的趋势使它不太适合作为在线学习算法。大脑解决这个问题的方法是，根据局部神经元和突触可获得的信息，决定自身的变化。这种自我修正的能力是一个经过长期进化过程微调的过程，是大脑学习和记忆的基础。
两个基本生物发现导致了许多在线学习算法的成功。首先，大脑中的神经元和突触保持着活动的历史痕迹。这些痕迹，被称为资格迹(eligibility traces)[3]。资格迹不会自动产生突触变化，但在自上而下的学习信号存在时会诱导突触可塑性。这也是第二个发现，大脑有大量自上而下的学习信号[4]，这些信号是大脑高级中枢在传递像奖励和惊喜等信息。这些自上而下的信号通常代表神经调节剂的活动，如多巴胺或乙酰胆碱。我们熟知的三因子学习规则其实也对应着这两个发现，资格迹是积累突触前和突触后神经元因子之间的联合相互作用，学习信号则是对应于全局调制信号。资格轨迹和自上而下的学习信号之间的相互作用使学习规则能够连接长时间尺度和短时间尺度之间的相互作用。
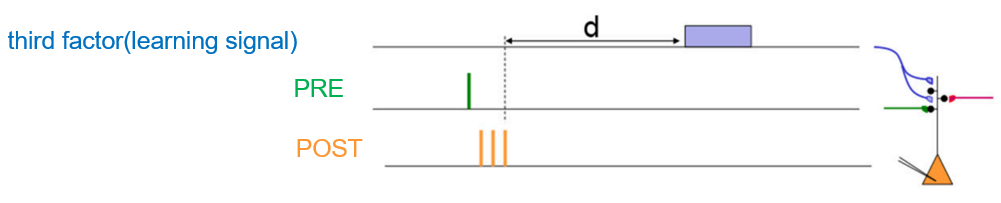图3. 三因子学习规则
E-prop[5]作为在线学习算法的代表性工作，它的目标是采用这两个成分，来合成突触可塑性，最小化损失函数。用公式表示即为，ejit 这个成分表示资格迹，它只跟踪局部的活动，特定于每个突触，例如突触前神经元i到突触神经元j的权重，并且也独立于损失函数。另一个，是自上而下的学习信号Ljt，它传输任务信息，这是特定于突触后神经元j，例如神经元。我们希望这个公式可以与基于梯度的学习联系起来，使得它有效对应于梯度下降。
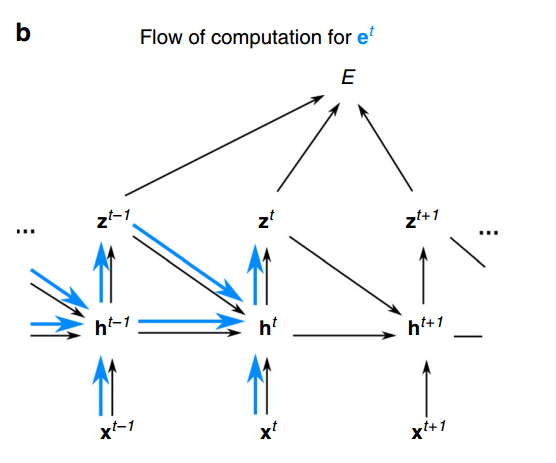
所以，我们从计算图开始，来观察资格迹和学习信号它们假设的数学形式。对于具有一层隐藏层的网络，我们用xt表示当前时间步t时神经元的输入，用ht表示神经元的隐藏状态，即表示当前时间步t的膜电压状态。zt表示时间步t的神经元输出，对于SNN它就是脉冲。我们应用随时间反向传播，计算损失函数相对权重的导数，可以写成计算每个时间步中损失函数相对于隐藏状态的导数以及隐藏状态相对于权重的导数的乘积，然后累加所有时间步，即Eq.(3)。如果我们在每个时间步的隐藏状态节点上应用链式法则，可以得到Eq.(4) 中稍微扩展的表达式，它对应于图5中的两条红色的计算流，一条是输出相对于隐藏状态的导数，一条是下一时间隐藏状态相对于当前时间步的导数。由于Eq.(4) 中包含下一个时间步中关于隐藏状态的损失的导数，我们可以用相同的方式分成两条计算流，迭代地执行这个操作。
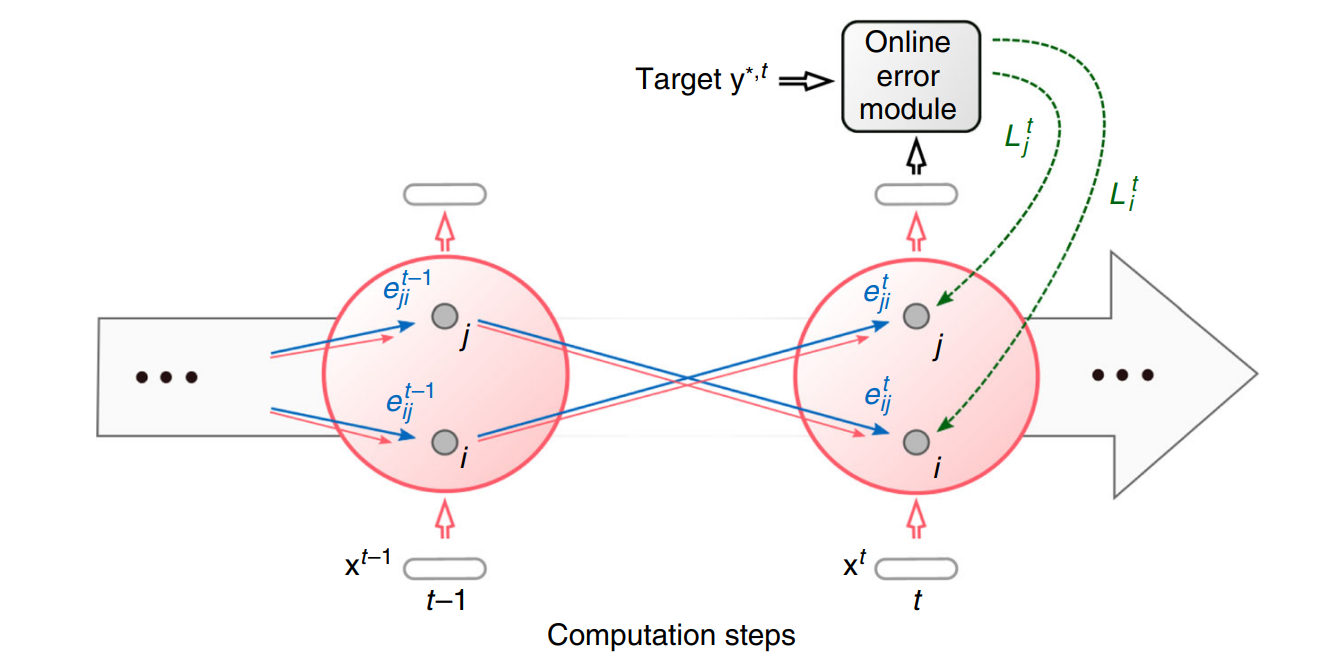图4. E-prop在线学习动态。资格迹的前馈计算用蓝色表示。根据Eq.(2)将资格迹与在线学习信号相结合
图5. 计算图和梯度传播
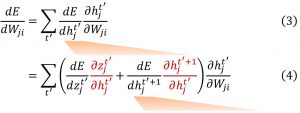
通过把前面迭代展开，交换求和顺序我们可以得到Eq.(2) 的表达式，在这里我们就可以赋予学习信号和资格迹的形式，绿色部分为学习信号，它实际上告诉我们改变当前时间步神经元的输出，对损失函数变化的影响，从图6中绿色的计算流可知，它除了直接影响损失函数，它还通过未来时间步的神经元的隐藏状态间接的影响损失函数。另一方面，资格迹，由表达式的其余蓝色部分表示，资格迹的作用是跟踪突触/权重W如何影响突触后神经元的隐藏状态hjt，并且这种影响根据突触后神经元的动力学随时间传播。由图6中蓝色的计算流可知，它可以由小于t的时间步递归计算，小于时间步t的梯度信息都是已知的，所以，它可以和网络前向传播过程一起计算。总体上，E-prop重写了BPTT相同的梯度，但分离出了与神经元特定动力学相关的部分并把它们总结为资格迹。
|
|
|
图6. 资格迹与学习信号的计算图
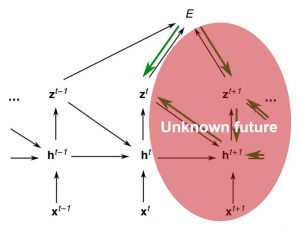
E-prop的目标是拥有一种可以与网络计算一起工作的学习算法，也就是在线的学习规则。但是，Eq.(5) 的学习信号实际上在时间步t是不可用的，因为神经元的输出也会影响其他神经元的未来隐藏状态，而我们没有办法在时间步t知道这一点。因此E-prop采用的方法是考虑近似值，将学习信号由全导数变成偏导数，也就是说因为资格迹中累积足够的时间信息，我们只考虑当前时间步的输出对于损失函数的影响。此时，学习信号被近似为瞬时损失乘上一个特定的权重矩阵。这个权重有两种选择策略：(1)神经元j到输出神经元k的突触连接的相应权重Wout的转置，即偏导数的计算结果；(2)将反馈对齐引入到循环网络中，采用一个随机固定的矩阵。虽然E-prop采用“剪枝”后的近似值，会偏离通过黑色传播获得的真实梯度，但是现在E-prop允许进行在线学习。
|
|
|
图7. 近似的学习信号
为了检验E-prop 进行时间信用分配的有效性，[5]进行一个实验模拟T型迷宫中啮齿动物的认知能力。在一个T型的迷宫装置，一只小鼠沿着迷宫底部移动，在前进的过程中，会有一系列的感觉线索沿着迷宫的左右排列。小鼠选择有线索数量比较多的一边会得到奖励。这个任务很难解决，因为小鼠必须认识到结果不受线索的呈现顺序或最后一个提示在哪一边的影响；而是独立于每一边的顺序来计算线索，并且必须比较总数来做出决定。学习困难的地方在于，解决这个问题的奖励直到做出决定后才会出现，所以小鼠必须在整个实验时间跨度内给它的行为分配信用，也就是说要知道从走迷宫开始，每个时间点对于它的决策的影响。由于奖励只有在决策期间给出，相应地，非零学习信号仅在决策期间才有定义，因此突触可塑性也只能在这个决策期间发生。那么在这么长的没有学习信号的期间，小鼠怎么学习去计数线索？
观察E-prop的计算图，时间步t时神经元j的发放可以通过两种不同的方式影响随后时间点t´>t时的损失函数E：
路径 (i)： 时间步t时神经元j的发放影响神经元j的隐藏变量的未来值(例如，其发放阈值)，这会影响t´时神经元j的发放，从而可能直接影响时间t´的损失函数。
路径 (ii)：时间步t时神经元j的发放影响t´时其他神经元j´的发放，直接影响t´时的损失函数。
由于学习信号由全导数变成偏导数，阻断了沿路径(ii)的梯度信息流。但资格迹使得路径(i) 保持畅通，它能够在学习信号变成非零之前，学习左右输入线索的响应差异，可以认为资格迹为梯度信息的传播提供了所谓的通向未来的高速公路。此外，实验通过应用Adaptive LIF(ALIF) 神经元，导致更持久的资格跟踪延伸到决策期，因此与学习信号相结合会导致突触可塑性，最终使网络能够学习这项任务。Adaptive LIF神经元具有自适应的阈值，脉冲发放后它的阈值会升高随时间缓慢衰减直到下一个脉冲发放它又升高，发放阈值是在较慢的时间尺度上变化，时间常数通常在几秒钟的范围内。神经元中这些较慢的过程对于获得与LSTM网络类似的强大计算能力的脉冲神经元至关重要。
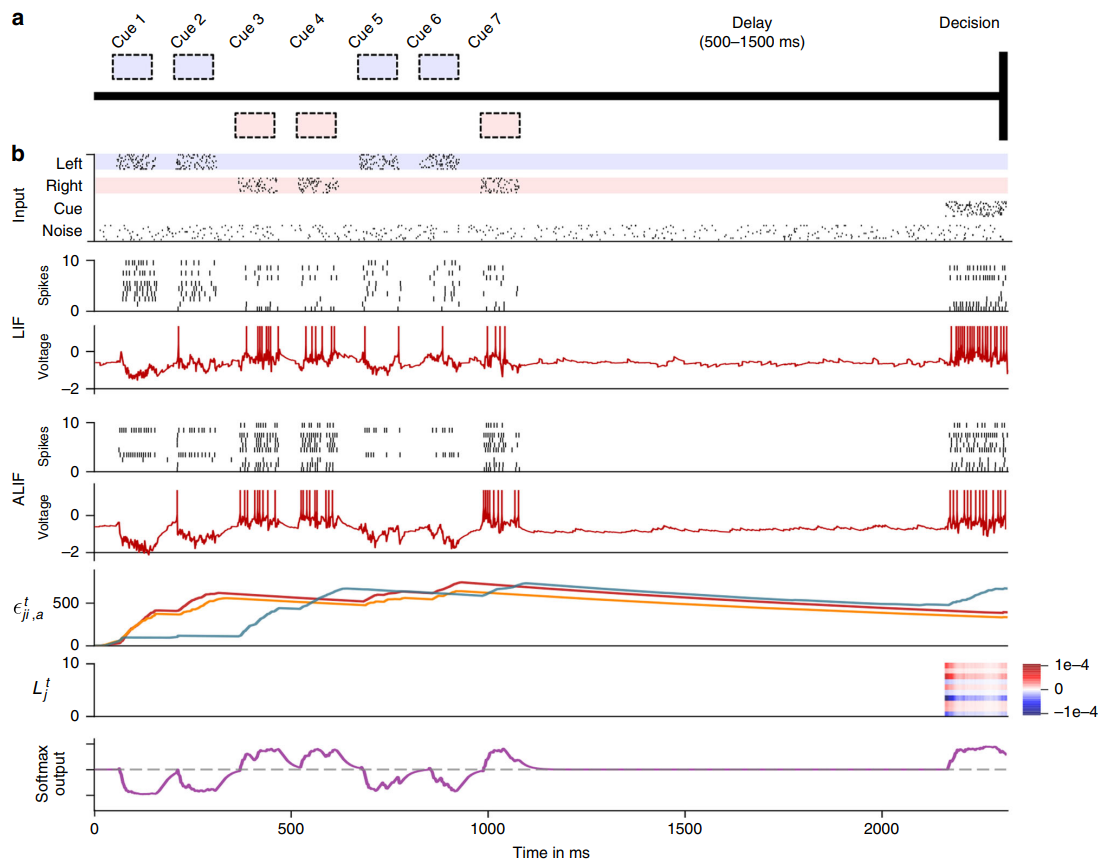
图8. 啮齿动物实验解决时间信用分配的任务。从上到下分别为：输入尖峰；50个LIF神经元中的10个样本和50个ALIF神经元中的10个样本的脉冲活动；两个样本神经元的膜电位；三个ALIF神经元样本的资格迹；10个样本神经元的学习信号和softmax网络输出。
学习规则也适用于机器学习中的任务，例如识别TIMIT数据集中的语音音素等，输入是语音信号，任务是识别每一帧的音素。如图9所示，使用相同的循环网络架构，使用E-prop训练的性能接近用随时间反向传播训练的网络。
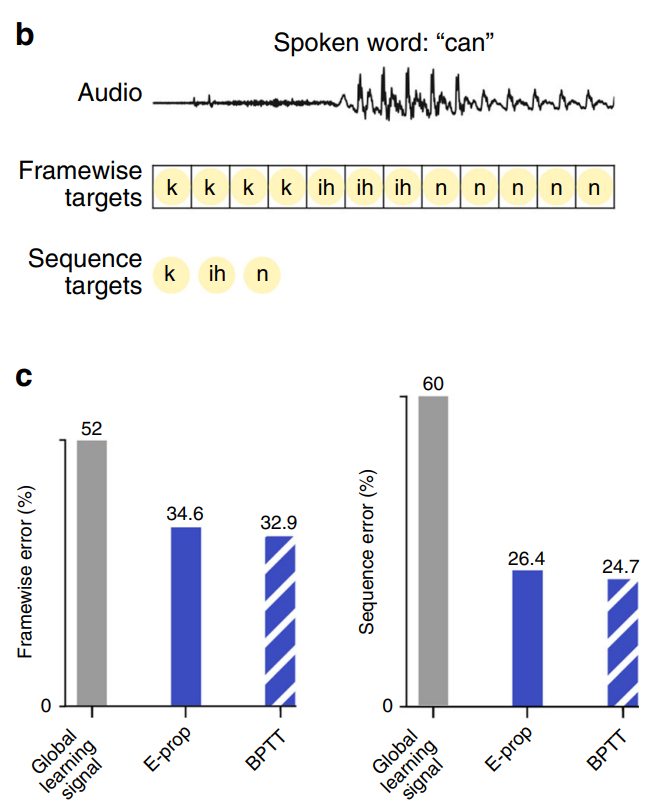
图9. BPTT与E-prop在音素识别学习中的比较
前面提到局部突触可塑性是由学习信号控制的，由于理想的学习信号在当前时间步不可用，因此采用网络输出产生的瞬时损失的随机预测。相比之下，突触可塑性在大脑中是通过多巴胺等学习信号来控制的，这些信号是由专门的大脑区域发出的，例如VTA（中脑腹侧被盖区，是两条主要的多巴胺神经通道的一部分），它会向大脑的不同神经网络发送统一的学习信号。这些专门大脑区域通过进化优化了学习信号，使得其他大脑区域能够表现出各种高级学习能力，从而能够快速学习与生存相关的任务。
图10. 大脑中的VTA
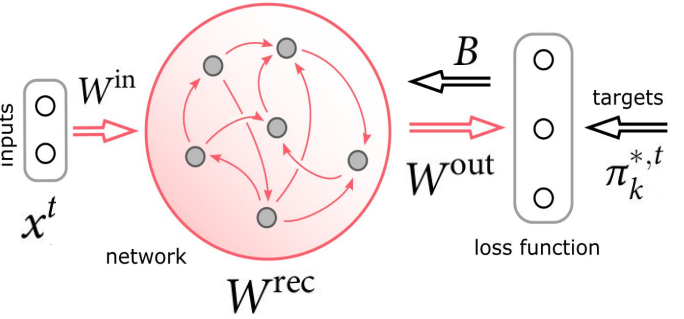
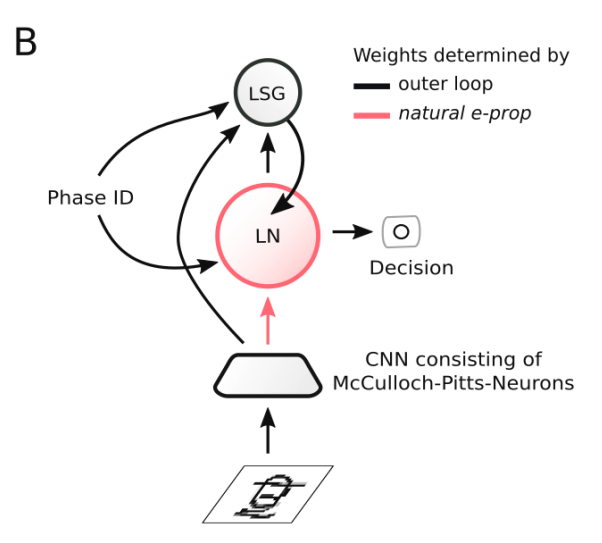
受这种生物的启发，[6]为E-prop人工建模一个VTA来发出学习信号，并称作学习信号发生器，该模块有单独的优化过程来促进快速学习，因此提出更好的学习信号，这些信号实际上是为可能遇到的任务量身定制的。由这种更像大脑的学习信号生成方法改进后的E-prop被称为Nature E-prop，结构上是由学习网络(LN)和学习信号生成器(LSG)组成，其中学习网络应用的是基于突触可塑性的学习规则，即Eq.(2)。
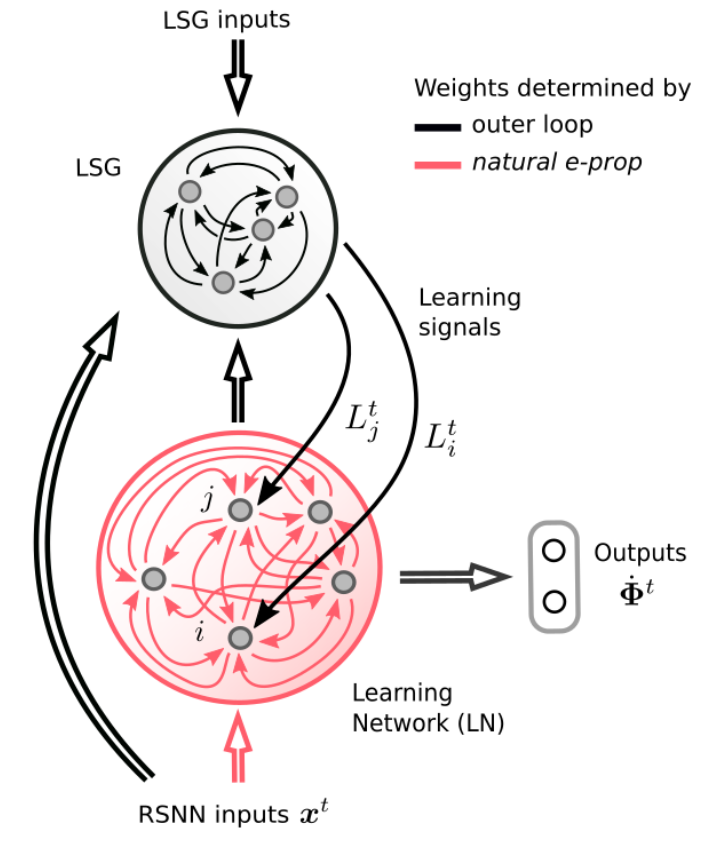
图11. Nature E-prop的通用架构
Nature E-prop的学习应用了标准的学习到学习(learning to learn, L2L)的范式，分为两个循环。通常认为有一个非常大的——通常是无限大的—— F族可能相关(具有某些共性)的学习任务。L2L的内部循环是在单个任务的层级上，LN从初始权重Winit开始学习特定的任务Ci，并根据突触可塑性规则更新这些权重，它使用学习信号是由LSG提供。L2L的外部循环是对于多个不同的任务，通过BPTT优化与LSG相关的突触权重以及LN的初始权重Winit。具体来说，整个流程分为两个阶段，第一阶段的学习，从F族随机抽取的许多任务C1，C2 … Cn，每个任务Ci上的学习性能由LN的输出计算损失函数进行评估，我们最小化损失E是在所有任务上的平均损失。该过程实际上是进行外循环的训练，其中优化是通过BPTT实现的。在第一阶段的学习之后，由外循环调节的所有参数都保持固定。第二阶段我们针对从中随机抽取的新任务Ci（在外循环没见过）评估LN的学习性能。
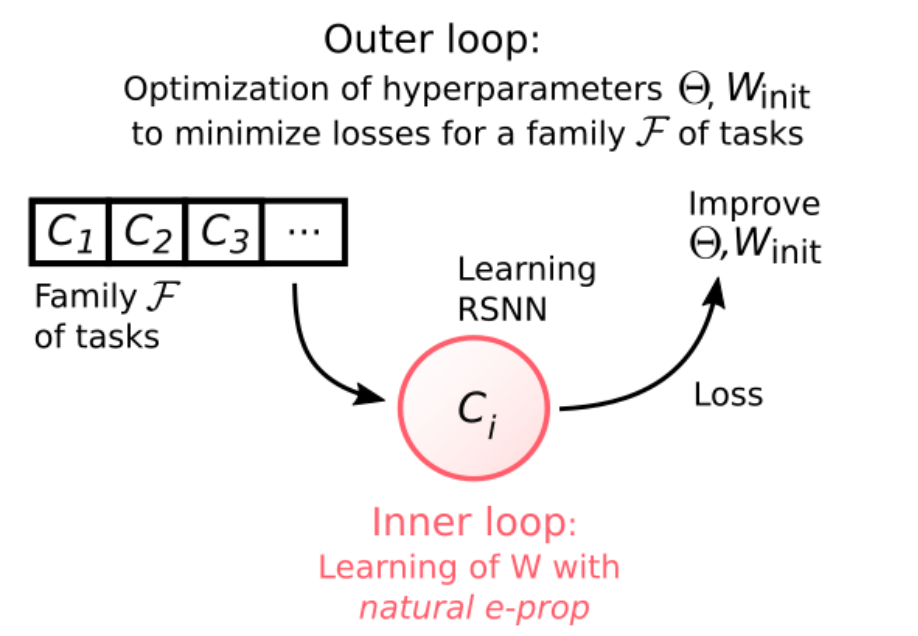
图12. L2L方案，内环路中使用突触可塑性
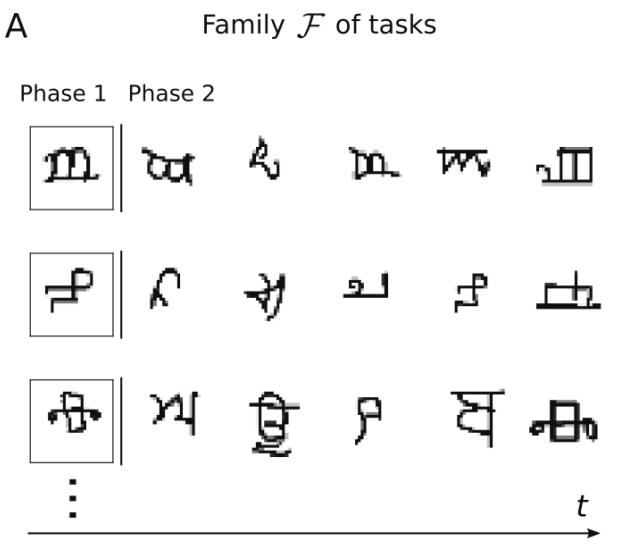
为了评估这个学习架构的实际学习速度，[6]进行字符挑战任务，这个任务被认为是构建更像人类的机器的一个挑战。该挑战使用Omniglot数据集，它实际上由来自许多不同字母的许多不同手写字符组成，除了一些不同类别的样本外，每个类别中也存在显着差异，因为可以以不同的方式绘制每个字符，因此它实际上是元学习的标准数据集。因为考虑的是少样本学习，这意味着网络应该能够仅仅通过查看此类类别的一个样本来了解什么是类别，因此，在Phase 1中，显示一个来自目标类别的样本，然后在Phase 2，将看到来自相同类别和其他新类别的样本，任务是网络必须立即决定每个样本是否与Phase 1的样本属于同一类。学习网络LN的输入是3层CNN的输出的01脉冲构成，它的权重是通过外循环优化。LN的输入xt还包含了Phase的ID，例如将Phase 1编码为0。LSG的输入包括样本的01编码以及LN的输出(神经元活动状态)，因为我们希望在Phase 1学习到什么是类别，LSG只有在Phase 1向LN发送学习信号，在Phase 1结束的时候发生基于突触可塑性的累积权重更新。
|
|
|
图13. 从单个样本中学习一类新的字符
在Phase 2期间，使用单个输出在线决定刚刚看到的字符是否与Phase 1中的字符属于同一类。使用加权和将RSNN的外部输入整合到神经元的膜电位中。LN的输出由来自LN中神经元的低通滤波脉冲序列的加权总和组成，以定性方式模拟LN中脉冲对下游神经元膜电位的影响。如图4所示，每个字符(包括阶段1中的字符)的呈现时间只有20毫秒，根据Eq.(2)的突触可塑性只发生一次，在试验的Phase 1结束时。见图14第二行，虚线表示的时间点上的模拟输出值，如果为正值，则判定刚刚看到的字符与Phase 1的字符属于同一类。
经过足够长时间的训练，Nature E-prop外环路测试错误率达到16.2%，接近人类错误率约为15%。这个结果表明，Nature E-prop是一种生物学上合理的学习方法，应用于相对较小的通用RSNN，能够以接近人类的性能水平解决这个少样本学习任务。
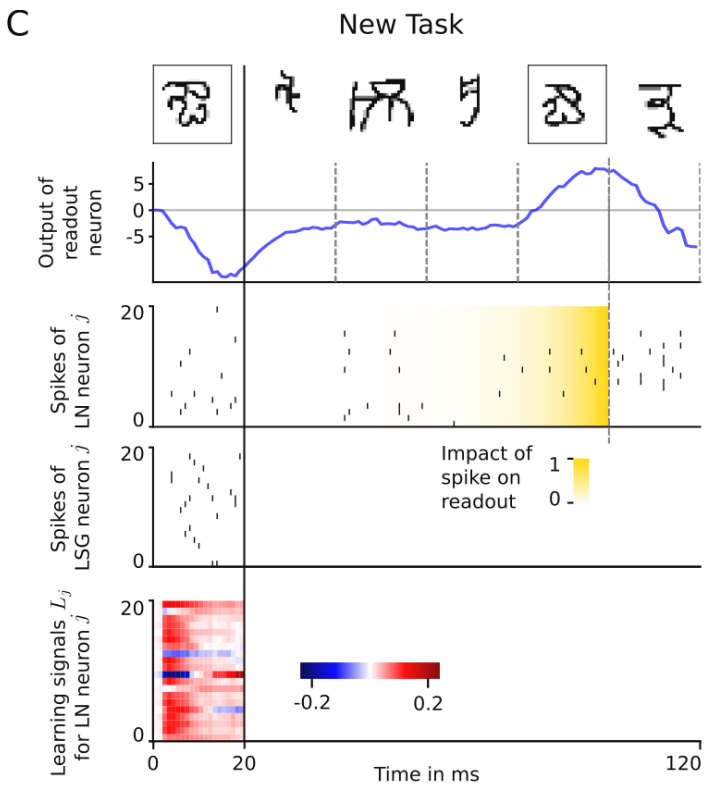
图14. Nature E-prop 少样本学习的样本实验
Summary
E-prop是对BPTT的近似，基于突触可塑性的局部在线学习规则。如果将突触可塑性的局部规则与来自一个独立网络的学习信号结合起来，该网络被优化为诱导RSNN的快速学习，那么少样本学习就以仿生的方式变得可行。
这种L2L的范式在神经形态硬件上实现快速片上学习同样具有可行性。外循环可以离线计算，优化SNN上超参数，以支持快速学习任意任务，然后将得到的超参数加载到芯片上。内循环只要简单的突触可塑性局部规则可以片上计算，从少量的样本中学习剩余的参数。然而，范式实现的难点在于离线启动阶段(L2L的外循环)的训练算法的有效性。要求更高的网络优化往往需要BPTT来进行SNN的离线优化。由于外循环是在许多任务上的平均损失进行反向传播，对于大规模SNN将造成训练困难的问题。
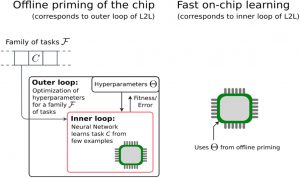
图15. L2L用于离线启动神经形态芯片的方案
References
- Christensen D V, Dittmann R, Linares-Barranco B, et al. 2022 roadmap on neuromorphic computing and engineering[J]. Neuromorphic Computing and Engineering, 2022, 2(2): 022501.
- Liao Q. Towards more biologically plausible deep learning and visual processing[D]. Massachusetts Institute of Technology, 2017.
- Gerstner, W., Lehmann, M., Liakoni, V., Corneil, D. & Brea, J. Eligibility traces and plasticity on behavioral time scales: experimental support of neohebbian three-factor learning rules. Front. Neural Circuits 12, 53 (2018).
- Yagishita, S. et al. A critical time window for dopamine actions on the structural plasticity of dendritic spines. Science 345, 1616–1620(2014).
- Bellec G, Scherr F, Subramoney A, et al. A solution to the learning dilemma for recurrent networks of spiking neurons[J]. Nature communications, 2020, 11(1): 3625.
- Scherr, F., Stöckl, C., & Maass, W., “One-shot learning with spiking neural networks”, bioRxiv, 2020.
