目录
一、前言
随着神经形态硬件(类脑芯片)的研究和发展,在边缘设备上实现在线上学习以适应设备漂移、环境变化、用户定制等应用场景,成为下一代人工智能的发展方向,而这依赖于高效的在线学习算法,能够实现在线实时的参数更新计算。传统深度神经网络(DNN)使用的反向传播(BP)算法在计算反向梯度时需要网络的全局信息,难以在时间维度上扩展。为研究可以支撑类脑芯片的高效片上学习,促进类脑芯片的发展和推广,需要研究并克服BP算法的四个问题:权重传输(weight transport)、非局部可塑性(non-local plasticity)、更新锁定(update locking)、全局损失函数(Global loss function)。
权重传输问题即误差的反向传播(back-propagating, BP)与生物脑中突触信号的单向传递矛盾[1,2]。在目标实现存算一体化的神经形态架构中,反向传播需要转移存储的数据,导致额外的能耗开销,给低能耗硬件框架上的片上学习带来巨大的挑战[3]。
非局部可塑性指BP学习需要输出端传回的全局误差信号,无法仅通过时间和神经元的局部信号更新权重。相反,生物神经元仅根据权重连接的两个神经元的即时激活即可完成学习 [4]。在神经形态计算中,BP的非局部可塑性不仅需要储存前馈计算过程中的所有变量,还必须计算并传播反向信号,大幅增加了存储需求和额外的操作和电路开销[5]。
更新锁定问题指BP网络的前馈过程与梯度反向传播过程不能同步进行,即在前馈过程中,权重更新将被锁定[6-8],导致学习速度降低,学习延迟增加。
全局损失函数是BP网络更新的核心目标。在监督学习中,损失函数的计算依赖于人为给定的标签。由于这类数据获取成本高,基于监督的BP学习难以对所有数据进行充分利用。尽管自监督学习可使用模型本身的信号计算全局损失[9-12],BP网络依旧容易过拟合于特定映射——对对抗攻击十分敏感[13,14],学习的特征也难以泛化于其他数据和任务[11]。
由于上述问题的存在,DNN所用的BP算法难以直接应用于在线学习领域。针对该问题,大量工作致力于寻找低功耗、低延时、低计算量、低内存需求的可在线更新的网络学习算法。目前,该领域的工作可大致分为两类:一是基于BP算法,利用网络特性和数学近似改善BP算法,降低内存需求,提高学习效率;二是采用仿生算法,模拟神经科学中神经细胞的生物特性实现网络参数更新和学习。许多仿生学习算法基于赫布理论,研究并发展出了一套仿生的人工神经网络学习算法。本文主要赫布学习算法的发展进行整理和介绍。
二、赫布学习算法
2.1赫布理论
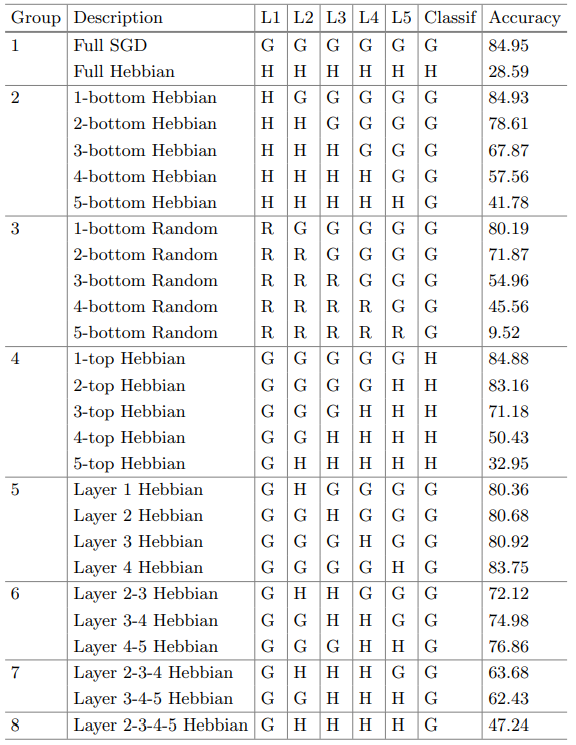 基于赫布理论的训练算法是一种仿生的局部学习算法,利用突触前和突触后神经元的局部可塑性规则更新神经元的连接权重。赫布理论的基本内容是:当一个神经元的轴突与另一个神经元接近且能刺激使其重复持续的兴奋时,这两个神经元或其中一个便会发生某些生长过程或代谢变化,致使二者的关联性增强。在人工神经网络中,神经元之间的关联性由二者的连接权重表示。同步激发的两个神经元,二者的权重增加;反之,则权重减少。在人工神经网络的训练中利用该可塑性,可以在不使用外界监督的情况下,引导网络学习提取有用的特征[15,16]。由于仅考虑局部突触的可塑性,赫布学习规避了基于BP算法的四大局限性,具有更好的生物可解释性。尽管已有大量工作对赫布学习进行了研究[14,17-20],为其在深度学习框架下的应用提供了宝贵的经验, 赫布学习仍然有尚未解决的问题。首先,现有的赫布网络均为浅层网络。随着网络深度的增加,赫布网络将迅速饱和,其特征提取能力几乎不再增加。其次,赫布网络的特征提取能力目前仍逊色于BP网络。表1[20]展示了6层采用不用训练方法得到的网络在CIFAR-10上的分类结果。其中“G”表示使用随机梯度下降(SGD)训练;“H”表示使用赫布理论更新层参数;“R”表示该层是未经训练的随机初始化状态。当网络全层采用SGD更新时,分类正确率最高。随着使用赫布更新的层数的增加,网络的分类正确率逐渐下降,但仍然优于未经训练的随机初始化状态。从该表格中可以看出,目前基于赫布理论的学习方法具有一定的有效特征提取能力,但仍然不如SGD。
基于赫布理论的训练算法是一种仿生的局部学习算法,利用突触前和突触后神经元的局部可塑性规则更新神经元的连接权重。赫布理论的基本内容是:当一个神经元的轴突与另一个神经元接近且能刺激使其重复持续的兴奋时,这两个神经元或其中一个便会发生某些生长过程或代谢变化,致使二者的关联性增强。在人工神经网络中,神经元之间的关联性由二者的连接权重表示。同步激发的两个神经元,二者的权重增加;反之,则权重减少。在人工神经网络的训练中利用该可塑性,可以在不使用外界监督的情况下,引导网络学习提取有用的特征[15,16]。由于仅考虑局部突触的可塑性,赫布学习规避了基于BP算法的四大局限性,具有更好的生物可解释性。尽管已有大量工作对赫布学习进行了研究[14,17-20],为其在深度学习框架下的应用提供了宝贵的经验, 赫布学习仍然有尚未解决的问题。首先,现有的赫布网络均为浅层网络。随着网络深度的增加,赫布网络将迅速饱和,其特征提取能力几乎不再增加。其次,赫布网络的特征提取能力目前仍逊色于BP网络。表1[20]展示了6层采用不用训练方法得到的网络在CIFAR-10上的分类结果。其中“G”表示使用随机梯度下降(SGD)训练;“H”表示使用赫布理论更新层参数;“R”表示该层是未经训练的随机初始化状态。当网络全层采用SGD更新时,分类正确率最高。随着使用赫布更新的层数的增加,网络的分类正确率逐渐下降,但仍然优于未经训练的随机初始化状态。从该表格中可以看出,目前基于赫布理论的学习方法具有一定的有效特征提取能力,但仍然不如SGD。
表1 不同参数更新方法对网络分类能力的影响
2.2经典赫布算法
经典赫布学习算法的更新公式非常简洁直白,即直接根据两个神经元之间的激活情况更新它们之间的连接权重。假设神经元的输出经过激活后在-1与1之间,则其更新公式如下:
其中为学习步长,和分别为两个神经元的激活值。可见,当神经元和同时为正或者为负时,说明二者的激活状态的是同步的,因此连接权重增加;反之,若两个神经元输出为一正一负时,说明二者为异步激活状态,连接权重降低。此外,神经元权重的更新幅度还受到神经元响应程度的影响。若某一个神经元的输出为0,说明该神经元处于未激活状态,相应的,权重不进行更新。原始的赫布学习仅考虑了两个神经元之间的关系,因此难以有效提取出不同维度的特征,即当网络退化为一个特定的模式时,经典赫布学习将不断强化单一模式,导致偏差增大。
2.2 WTA算法
由于相邻神经元之间具有竞争性,不同神经元之间的连接也是相互影响的,如已在哺乳动物的大脑皮层中发现神经元通过抑制侧向神经元以竞争神经元间连接的回路[6,7],这种神经元之间的竞争现象被称为winner-take-all (WTA)。在WTA算法中,每次更新仅有同步性最高的神经元之间的连接会被加强,如下所示:
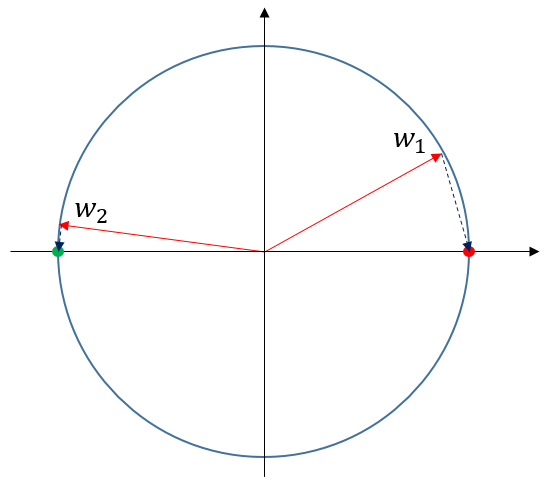 其中为当前层的输入信号,该层的个神经元竞争对响应最强的神经元作为胜者(与内积最小)。仅有胜者神经元可以在当次学习中更新参数,增强其与的响应。当下次收到与相似的输入信号时,神经元的响应将会更强,更容易在神经元竞争中胜出,并通过权重更新进一步加强对该信号的响应能力。这一特点使WTA能够更容易提取到输入信号的显著特征。如图1所示,在WTA算法的更新规则下,不同神经元权重向量将会逐渐靠近不同的输入信号。
其中为当前层的输入信号,该层的个神经元竞争对响应最强的神经元作为胜者(与内积最小)。仅有胜者神经元可以在当次学习中更新参数,增强其与的响应。当下次收到与相似的输入信号时,神经元的响应将会更强,更容易在神经元竞争中胜出,并通过权重更新进一步加强对该信号的响应能力。这一特点使WTA能够更容易提取到输入信号的显著特征。如图1所示,在WTA算法的更新规则下,不同神经元权重向量将会逐渐靠近不同的输入信号。
图 1 WTA算法更新示意图
2.3 SoftHebb算法
[14]则在WTA算法基础上使用softmax和余弦距离控制不同神经元之间的更新权重,提出了SoftHebb算法,并且为网络的学习过程提供了贝叶斯解释。其仿赫布可塑性规则能够最小化模型概率分布与输入的K-L散度,同时,在特定假设下,最小化与标签的交叉熵。在单层网络中,SoftHebb可以显著提高学习速度和鲁棒性,大幅提升应对对抗攻击的能力。其更新过程如下:
其中表示神经元的权重与输入之间的余弦距离,表示神经元的偏置参数,则是神经元的输出经过softmax非线性运算后的结果。的更新公式则为:
2.4 多层赫布网络
尽管已有很多工作为赫布学习的发展和完善做出了贡献,但大部分工作主要考虑单层网络的特性分析,赫布网络依旧容易饱和。[21]在前人工作的基础上加入了反赫布可塑性(soft anti-hebb plasticity),自适应学习率和尺度变换。反赫布可塑性学习使异步激活的神经元连接权重降低,结合SoftHebb的思路,通过softmax对异步激活值进行加权,使得同步性最差的神经元连接具有更高的更新权重。其更新规则如下:
其中是突触前神经元的激活值,是第个神经元的总输入权重。
自适应学习率可在训练中根据连接权值的大小自动调整调整学习步长。根据上述权重学习规则,随着学习的进行,神经元间的权重向量模长将趋向于1。因此,当权重向量模大于1时,学习步长应该更大,其定义如下:
其中为初始学习率,为控制学习率变化的超参数。
尺度变换规则使得图像每经过一个SoftHebb层,将通过池化操作进行一次下采样,使得网络能够获得更高的感受野,从而统合更大尺度的信息。
在[21]的改进下,基于赫布学习的网络从原本的1层扩展到3层,但是相比于DNN的深度,仍然有很多研究和提升的空间。
三、总结
本文首先分析了BP算法在在线学习中应用的局限性,然后介绍了仿生学习算法中的赫布学习算法:模仿生物神经元的局部可塑性规则,通过相邻神经元的激活状态实现神经元权重的更新。对经典赫布学习以及发展出来的三种变式进行了介绍。除了赫布学习外,还有很多其他的仿生学习算法。目前的仿生学习算法尽管具有更好的生物可解释性与更低的能量-时间成本,在不考虑计算开销与数据限制的情况下,与传统BPTT的性能相比仍有提升空间。为实现在线学习的应用需求,克服BPTT在在线学习中的限制,对仿生学习算法的研究仍会继续,未来还会整理其他的仿生学习工作并分享给大家。
参考文献
[1] Grossberg, S. Competitive learning: From interactive activation to adaptive resonance. Cognitive science, 11(1): 23-63, 1987.
[2] Crick, F. The recent excitement about neural networks. Nature, 337(6203): 129-13, 1989.
[3] Crafton, B., West, M., Basnet, P., Vogel, E., and Raychowdhury, A. Local learning in rram neural networks with sparse direct feedback alignment. In IEEE/ACM International Symposium on Low Power Electronics and Design (ISLPED), pages 1-6, 2019.
[4] Baldi, P., Sadowski, P., and Lu, Z. Learning in the machine: The symmetries of the deep learning channel. Neural Networks, 95: 110-133, 2017.
[5] Lowe, S., O’Connor, P., and Veeling, B. Putting an end to end-to-end: Gradient-isolated learning of representations. Advances in neural information processing systems, 32, 2019.
[6] Czarnecki, W. M., Swirszcz, G., Jaderberg, M., Osindero, S., Vinyals, O., and Kavukcuoglu, K. Understanding synthetic gradients and decoupled neural interfaces. In International Conference on Machine Learning, pages 904-912, 2017.
[7] Jaderberg, M., Czarnecki, W. M., Osindero, S., Vinyals, O., Graves, A., Silver, D., and Kavukcuoglu, K. Decoupled neural interfaces using synthetic gradients. In International conference on machine learning, pages 1627-1635, 2017.
[8] Frenkel, C., Lefebvre, M., and Bol, D. Learning without feedback: Fixed random learning signals allow for feedforward training of deep neural networks. Frontiers in neuroscience, page 20, 2021.
[9] Chen, T., Kornblith, S., Norouzi, M., and Hinton, G. A simple framework for contrastive learning of visual representations. In International conference on machine learning, pages 1597-1607. 2020.
[10] Mitrovic, J., McWilliams, B., Walker, J., Buesing, L., and Blundell, C. Representation learning via invariant causal mechanisms. ArXiv: 2010.07922, 2020.
[11] Lee, H., Lee, K., Lee, K., Lee, H., and Shin, J. Improving transferability of representations via augmentation-aware self-supervision. Advances in Neural Information Processing Systems, 34, 2021.
[12] Tomasev, N., Bica, I., McWilliams, B., Buesing, L., Pascanu, R., Blundell, C., and Mitrovic, J. Pushing the limits of self-supervised resnets: Can we outperform supervised learning without labels on imagenet? ArXiv: 2201.05119, 2022.
[13] Madry, A., Makelov, A., Schmidt, L., Tsipras, D., and Vladu, A. Towards deep learning models resistant to adversarial attacks. ArXiv:1706.06083, 2017.
[14] Moraitis, T., Toichkin, D., Chua, Y., and Guo, Q. Softhebb: Bayesian inference in unsupervised hebbian soft winner-take-all networks. ArXiv:2107.05747, 2021.
[15] Sanger, T. D. optimal unsupervised learning in a single-layer linear feedforward neural network. Neural networks, 2(6): 459-473, 1989.
[16] Linsker, R. Local synaptic learning rules suffice to maximize mutual information in a linear network. Neural Computation, 4(5): 91-02, 1992.
[17] Von der Malsburg, C. Self-organization of orientation sensitive cells in the striate cortex. Kybernetik, 14(2): 85-100, 1973.
[18] Nessler, B., Pfeiffer, M., Buesing, L., and Maass, W. Bayesian computation emerges in generic cortical microcircuits through spike-timing-dependent plasticity. PLoS computational biology, 9(4): e1003037, 2013.
[19] Diehl, P. U. and Cook, M. Unsupervised learning of digit recognition using spike-timing-dependent plasticity. Frontiers in computational neuroscience, 9:99, 2015.
[20] Amato, G., Carrara, F., Falchi, F., Gennaro, C., Lagani, G. Hebbian Learning Meets Deep Convolutional Neural Networks. Image Analysis and Processing (ICIAP): 324-334, 2019.
[21] Adrien Journe, Hector Garcia Rodriguez, Qinghai Guo, Timoleon Moraitis. Hebbian Deep Learning Without Feedback. ArXiv: 2209.11883, 2022.